
Visto che delle problematiche legate al Covid-19 ne ho parlato diffusamente nei mesi scorsi fino alla noia, quando la cosa a molti sembrava chiusa, oggi che il mondo riscopre il virus, io vi annoierò con un altro argomento: la matematica!
Quindi metto subito le carte in tavola: questo post ha più fini didattici che non considerazioni operative dirette su uno specifico prodotto. Ci sarà un po’ di matematica, nulla di sconvolgente, ma soprattutto cercheremo di come utilizzare, se e quando, la leva finanziaria.
Fin dall’inizio vi dico che io la uso pochissimo, sostanzialmente perché non è il mio stile, ma è sicuramente una delle tante soluzioni che un trader può utilizzare.
Partiamo dalla versione più semplice:
La leva fissa ed effetto compounding
Questo è il caso tipico di molti ETF che magari qualche volta avete utilizzato. Avrete visto che tipicamente hanno nomi che terminano con … Long 5X. Significa che questo ETF replicherà le variazione del sottostante amplificandole 5 volte, mentre se fosse stato Short lo avrebbe replicato in senso opposto, ossia l’ETF sale quando il sottostante scende e viceversa. Niente di complicato direte voi. Ad esempio prendiamo un ETF Long 5X sul FTSE-MIB e guadagneremo o perderemo 5 volte quello che fa l’indice stesso.
Dopo di che pero succede una cosa strana prendiamo un ETF con il FTSE-MIB a 19000 punti, l’indice fa un po’ di su e giù e dopo qualche giorno ve lo trovate a 19500 punti. Tutti contenti andate a vendere il vostro ETF pensando di portare a casa un bel gruzzolo ed invece sorpresa: l’ETF ha un prezzo inferiore a quello a cui lo avete acquistato! Vi hanno fregato? No, è la matematica bellezza! Traduciamo quanto detto in formula chiamiamo:
-
S(t) il prezzo del sottostante al tempo t.
-
a(t) la variazione del prezzo del sottostante al tempo t rispetto al prezzo t-1
-
D(t) il prezzo del derivato al tempo t.
-
L la leva del derivato
possiamo quindi affermare che:
S(t+1) = (1+a(t))S(t) e di conseguenza
D(t+1) = (1+L a(t))D(t).
noterete che se L=1 S(t) ha la stessa formula di D(t), giustamente tra le due formule c’è solo un fattore L di differenza. Ora supponiamo che il nostro indice faccia il primo giorno +10% ed il secondo -10% (sono naturalmente simulazioni numeriche, non mi aspetto che l’indice abbia una tale volatilità).
Questo vuol dire che:
S(1) = 1,1S(0) e S(2) = 0,9S(1) quindi
S(2) = 1,1*0,9S(0) = 0,99S(0)
Qui per alcuni ci potrebbe essere una sorpresa: anche su un giorno guadagno un 10% ed il giorno successivo lo riperdo non ho fatto pari, ma ho perso un 1%. Perché? Semplicemente perché la perdita si applica ad un capitale maggiore di quella a cui ho applicato il guadagno. Questo dovrebbe farvi capire perché è più importante limitare le perdite che non spingere l’acceleratore sul rischio.
OK, questo è chiaro, perciò con una leva fissa 5X avremmo perso il 5%? Purtroppo la risposta è nuovamente no. Applichiamo la formula con leva:
D(1) = (1+0,1*5)D(0) = 1,5D(0) e D(2) = (1-0,1*5)D(1) = 0,5*D(1) quindi:
D(2) = 0,5*1,5D(0) = 0,75D(0)
Ossia non abbiamo perso il 5%, bensì il 25%! Ecco l’effetto compounding nella pratica: in altre parole ci troviamo con il 75% del capitale iniziale. Chiaro come si può rapidamente bruciare il capitale? Per questo il consiglio a chi utilizzi tali strumenti di non tenere le posizioni aperte per pochi giorni, meglio ancora se intraday, perché basta prendere una giornata storta e diventa poi veramente difficile andare a recuperare la posizione.
Qui sotto vi ho riportato una simulazione di una serie numerica più lunga:
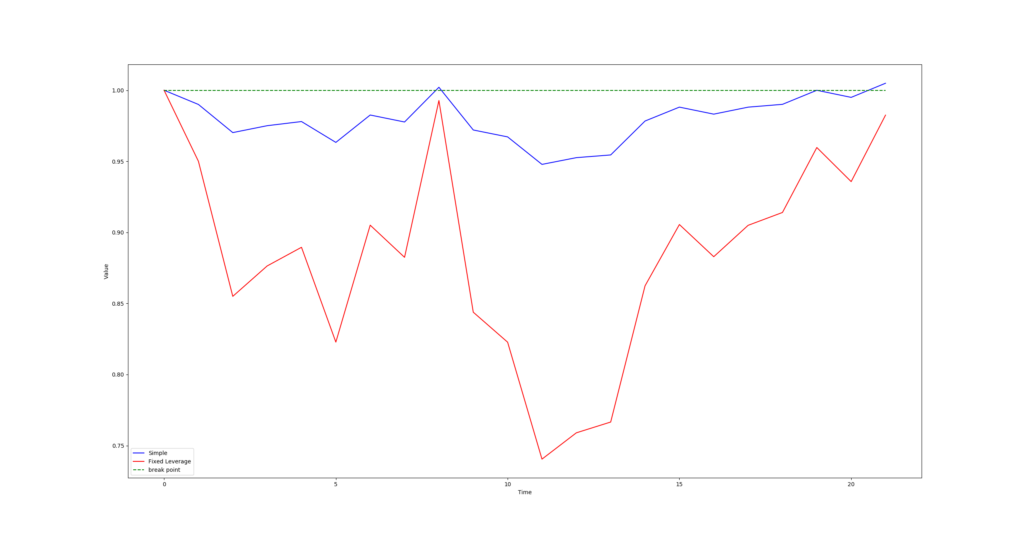
Ormai avrete capito il giochetto: basta sostituire ricorsivamente le variazioni di prezzo moltiplicate per la leva per ottenere la variazione totale. Nella serie sopra riportata viene evidenziato il caso citato all’inizio, in cui qualcuno di voi magari sarà incappato: il nostro indice si è portato in territorio positivo mentre l’ETF è lì che arranca sotto la pari.
Per ora è tutto, vi sarete già annoiati abbastanza. Nella prossima puntata vedremo come esistano strumenti dotati di leva che eviti l’effetto compounding, strumento che ho utilizzato in questa strategia che è ancora aperta.
L’ultima raccomandazione che sento di fare è: approfondite sempre gli strumenti che utilizzate, non siate mai superficiali perché la superficialità e il modo migliore per dilapidare il proprio capitale.
Naturalmente, se avete qualche domanda fatela tranquillamente qui sotto.
Spero di aver fatto cosa gradita lasciando link diretti a tutti i dati senza passare per servizi di pubblicità. Per questo mi auguro che siate così gentili, vista la completa gratuità del sito, di condividere l’articolo sui social, mettere un like o sostenere il blog in altro modo se l’articolo è di vostro gradimento.
Vi ricordo che chiunque voglia essere tempestivamente informato sulle novità pubblicate dal blog può iscriversi alla mailing list qui a destra. Inoltre tenete presente che l’iscrizione è portata a termine solo se viene confermata dopo aver cliccato sul link che vi verrà spedita a seguito dell’immissione della vostra email alla mailing list.